vivid: Variable Importance and Variable Interaction Displays

Introduction

Introduction to vivid

Variable importance (VImp), variable interaction measures (VInt) and partial dependence plots (PDPs) are important summaries in the interpretation of statistical and machine learning models. In this vignette we describe new visualization techniques for exploring these model summaries. We construct heatmap and graph-based displays showing variable importance and interaction jointly, which are carefully designed to highlight important aspects of the fit. We describe a new matrix-type layout showing all single and bivariate partial dependence plots, and an alternative layout based on graph Eulerians focusing on key subsets. Our new visualisations are model-agnostic and are applicable to regression and classification supervised learning settings. They enhance interpretation even in situations where the number of variables is large and the interaction structure complex. Our R package vivid (variable importance and variable interaction displays) provides an implementation. When referring to VImp and VInt together, we use the shorthand VIVI. For more information related to visualising variable importance and interactions in machine learning models see our published work[1].

Install instructions

Some of the plots used by vivid are built upon the zenplots package which requires the graph package from BioConductor. To install the graph and zenplots packages use:

if (!requireNamespace("graph", quietly = TRUE)){ install.packages("BiocManager") BiocManager::install("graph")
} install.packages("zenplots")

Now we can install vivid by using:

install.packages("vivid")

Alternatively you can install the latest development version of the package in R with the commands:

if(!require(remotes)) install.packages('remotes') remotes::install_github('AlanInglis/vividPackage')

We then load the vivid package via:

library(vivid) 

Background

VIVI metrics can be categorized into two types: those that are model-specific (embedded) and those that are model-agnostic. Here we provide a brief background on variable importance, variable interactions, and partial dependence and discuss their use in vivid.

Variable Importance

The importance value of a variable measures the extent to which it impacts the model’s output. Embedded methods weave variable importance directly into the machine learning algorithm. For instance, machine learning methods like random forests (RF)[2] and gradient boosting machines (GBM)[3] utilize their tree-based architecture to evaluate the performance of the model. Similarly, Bayesian additive regression tree models (BART)[4] adopt an embedded approach to yield VIVI metrics by measuring the proportion of splitting rules for for individual or paired variables in the trees.

The package randomForestExplainer[5] offers a toolkit for deciphering the inner workings of a random forest. It applies the minimal depth concept[6] to gauge both the significance and interaction strength by observing a variable’s location within the trees. Moreover, the varImp package[7] facilitates the computation of importance scores for the party package’s conditional inference random forest[8]. For gradient boosted machines, the EIX[9] package can be used to calculate VIVI, and graphically represent the findings.

Model-agnostic techniques are universally applicable to any ML algorithm. These methods offer flexibility in model choice and are valuable for comparing various ML models. Permutation importance[2], a model-agnostic method, assesses VImps by computing the change in a model’s predictive accuracy after permuting a variable. This approach is available in the iml[10], flashlight[11], DALEX[12], and vip[13] packages.

In vivid we provide the functionality to calculate either an agnostic or model-specific importance.

1. To calculate agnostic importance, vivid uses a permutation approach[14]. In this approach, the model’s error score (e.g., root mean square error) is first determined. Afterward, each feature is randomly permuted, and the error score is computed again. The change in performance indicates the importance score of that particular feature. The permutation algorithm can be described in the following:

Permutation Importance Algorithm:

Input: Fitted predicted model \(m\), dataset \(D\)

Compute: Compute error score \(w_{k}\) of the fitted model \(m\) on data \(D\).

For each feature \(k\) (column of \(D\))

• For each repetition \(r\) in \(1,...,R\):
  1. Randomly shuffle column \(k\) of dataset \(D\) to generate a shuffled version of the data.
  2. Compute the score \({w}^*_{r,k}\) of model \(m\) on shuffled data.
• Compute importance \(\texttt{imp}_k\) for feature \(f_k\) defined as:

\[\begin{equation} \tag{1} \texttt{imp}_k = w_{k} - \frac{1}{R}\sum_{r = 1}^Rw^*_{rk} \end{equation}\]

2. For model-specific variable importance, we provide individual methods to access importance scores for some of the most popular model fitting R packages, namely; ranger[15], mlr[16], mlr3[17], and parsnip[18]. See Section Model Fits for more details on using different models with vivid.

Partial Dependence

Friedman (2000)[19] introduced Partial Dependence Plots (PDPs) as a model-agnostic method to visualize the relationship between a chosen predictor and the model outcome, while averaging out the effects of other predictors. Individual Conditional Expectation (ICE) curves, introduced by Goldstein et al. (2015)[20], depict the relationship between a specific predictor and the model outcome by setting other predictors at certain observation levels. Essentially, PDPs represent the averaged outcome of all ICE curves in the dataset. The iml, DALEX, flashlight, and pdp[21] R packages offer PDP functionalities, while the ICEbox package[20] caters to ICE curves and their variations. The partial dependence of the model fit function \(g\) on predictor variables \(S\) (where \(S\) is a subset of the \(p\) predictor variables) is estimated as:

\[\begin{equation} \tag{2} f_S(\mathbf{x}_S)=\frac{1}{n}\sum^n_{i=1}g(\mathbf{x}_s,\mathbf{x}_{C_i}) \end{equation}\]

where \(C\) denotes predictors other than those in \(S\), \({x_{C_1},x_{C_2},...,x_{C_n}}\) are the values of \(x_C\) occurring in the training set of n observations, and \(g()\) gives the predictions from the machine learning model. For one or two variables, the partial dependence functions \(f_S(\mathbf{x}_S)\) are plotted (a so-called PDP) to display the marginal fits.

Variable Interactions

For VInts, the H-statistic by Friedman and Popescu (2008)[22] is a model-agnostic measure that gauges interactions using partial dependence. It contrasts the joint effects of a variable pair with the sum of their marginal effects.. This is implemented in the iml and flashlight packages and is defined as:

\[\begin{equation} \tag{3} H^2_{jk}=\frac{\sum^n_{i=1}[f_{jk}(x_{ij},x_{ik})-f_j(x_{ij})-f_k(x_{ik})]^2}{\sum^n_{i=1}f^2_{jk}(x_{ij},x_{ik})} \end{equation}\]

However, when the denominator in Equation 2 is small, the partial dependence of variables \(j\) and \(k\) remains constant. As a result, minor variations in the numerator can produce spuriously high \(H\)-values. Consequently, in vivid we use the the unnormalized \(H\)-Statistic to calculate the pair-wise interaction strength. The unnormalized version of the \(H\)-statistic was chosen to have a more direct comparison of interaction effects across pairs of variables by reducing the identification of spurious interactions and gives the results of \(H\) on the scale of the response (for regression).

\[\begin{equation} \tag{4} H_{jk}=\sqrt{\frac{1}{n}\sum^n_{i=1}[f_{jk}(x_{ij},x_{ik})-f_j(x_{ij})-f_k(x_{ik})]^2} \end{equation}\]

Data and Model

Data used in this vignette

The data used in the following examples is simulated from the Friedman benchmark problem[23]. This benchmark problem is commonly used for testing purposes. The output is created according to the equation:

\[\begin{equation} \tag{5} y = 10 sin(π x_1 x_2) + 20 (x_3 - 0.5)^2 + 10 x_4 + 5 x_5 + e \end{equation}\]

For the following examples we set the number of features to equal 9 and the number of samples is set to 350 and fit a randomForest random forest model with \(y\) as the response. As the features \(x_1\) to \(x_5\) are the only variables in the model, therefore \(x_6\) to \(x_{9}\) are noise variables. As can be seen by the above equation, the only interaction is between \(x_1\) and \(x_2\)

Create the data:

set.seed(101)
genFriedman <- function(noFeatures = 10, noSamples = 100, sigma = 1) {
  
  # Create dataframe with named columns
  df <- setNames(as.data.frame(matrix(runif(noSamples * noFeatures, 0, 1), nrow = noSamples), 
                               stringsAsFactors = FALSE), 
                 paste0("x", 1:noFeatures))
  
  # Equation: y = 10sin(πx1x2) + 20(x3−0.5)^2 + 10x4 + 5x5 + ε
  
  df$y <- 10 * sin(pi * df$x1 * df$x2) + 
    20 * (df$x3 - 0.5)^2 + 
    10 * df$x4 + 
    5 * df$x5 + 
    rnorm(noSamples, sd = sigma) # error
  
  return(df)
}

myData <- genFriedman(noFeatures = 9, noSamples = 350, sigma = 1) 

Model Fit

Part of the intention behind vivid was to create a package that facilitated ease of use coupled with the flexibility to use the agnostic VIVI methods on a wide range of machine learning (ML) models. Section Model Fits provides practical examples of how to use vivid with some of the more popular ML algorithms. For brevity, for the following examples, we create a random forest fit from the randomForest package to use with vivid.

library(randomForest) # for model fit
set.seed(1701)
rf <- randomForest(y ~ ., data = myData)

vivi

vivi function

The vivi function calculates both the importance and interactions using S3 methods. By default, the agnostic importance and interaction scores in vivid are computed using the generalized predict function from the condvis2 package. Consequently, vivid can be used out-of-the-box with any model type that works with condvis2 predict (see CVpredict from condvis2 for a full list of compatible model types). To allow vivid to run with other model fits, a custom predict function must be passed to the predictFun argument (as discussed in the Section Custom Predict Function).

The vivi function first computes variable importance and interactions for a fitted model, then produces a square, symmetrical matrix that contains variable importance on the diagonal and variable interactions on the off-diagonal.

The vivi function requires three inputs: a fitted machine learning model, a data frame used in the model’s training, and the name of the response variable for the fit. The resulting matrix will have importance and interaction values for all variables in the data frame, excluding the response variable. By default, if no embedded variable importance method is available or selected, an agnostic permutation method is applied. For clarity, this is shown in the importanceType = 'agnostic' argument below. For an example of using embedded methods, see Section Embedded VImps.

Any variables that are not used by the supplied model will have their importance and interaction values set to zero. While the viviHeatmap and viviNetwork visualization functions (seen in the Section Visualisations) are tailored for displaying the results of vivi calculations, they can also work with any square matrix that has identical row and column names. (Note, the symmetry assumption is not required for viviHeatmap and viviNetwork uses interaction values from the lower-triangular part of the matrix only.) To see a description of all function arguments use: ?vivid::vivi()

set.seed(1701)
viviRf  <- vivi(fit = rf, 
                data = myData, 
                response = "y",
                gridSize = 50,
                importanceType = "agnostic",
                nmax = 500,
                reorder = TRUE,
                predictFun = NULL,
                numPerm = 4,
                showVimpError = FALSE)

Visualisations

Visualizing the results

NOTE: If viewing this vignette from the vivid CRAN page, then some images may not format correctly. It is recommended to view this vignette on GitHub via the following link: https://alaninglis.github.io/vivid/articles/vividVignette.html

Heatmap plot

The viviHeatmap function generates a heatmap that displays variable importance and interactions, with importance values on the diagonal and interaction values on the off-diagonal. The function only requires a vivid matrix as input, which does not need to be symmetrical. Additionally, color palettes can be specified for both importance and interactions via the impPal and intPal arguments. By default, we have opted for single-hue, color-blind friendly sequential color palettes developed by Zeileis et al[24]. These palettes represent low and high VIVI values with low and high luminance colors, respectively, which can aid in highlighting pertinent values.

The impLims and intLims arguments determine the range of importance and interaction values that will be assigned colors. If these arguments are not provided, the default values will be calculated based on the minimum and maximum VIVI values in the vivid matrix. If any importance or interaction values fall outside of the specified limits, they will be squished to the closest limit. For brevity, only the required vivid matrix input is shown in the following code. To see a description of all the function arguments, see ?vivid::viviheatmap()

viviHeatmap(mat = viviRf)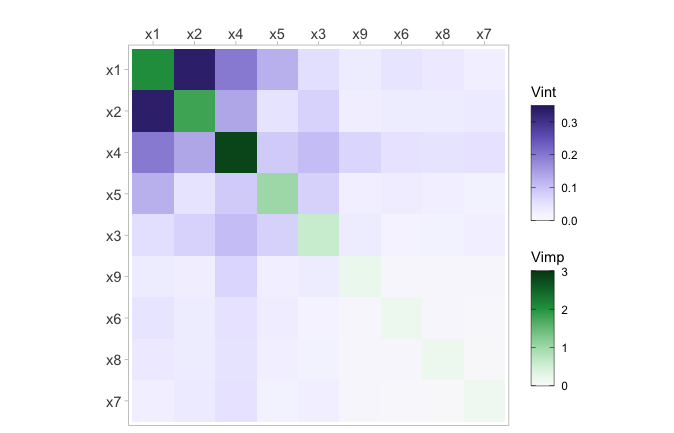

Figure 1: Heatmap of a random forest fit displaying 2-way interaction strength on the off diagonal and individual variable importance on the diagonal. \(x_1\) and \(x_2\) show a strong interaction with \(x_4\) being the most important for predicting \(y\).

Network plot

With viviNetwork, a network graph is produced to visualize both importance and interactions. Similar to viviHeatmap, this function only requires a vivid matrix as input and uses visual elements, such as size and color, to depict the magnitude of importance and interaction values. The graph displays each variable as a node, where its size and color reflect its importance (larger and darker nodes indicate higher importance). Pairwise interactions are displayed through connecting edges, where thicker and darker edges indicate higher interaction values.

To begin we show the network using default settings.

viviNetwork(mat = viviRf)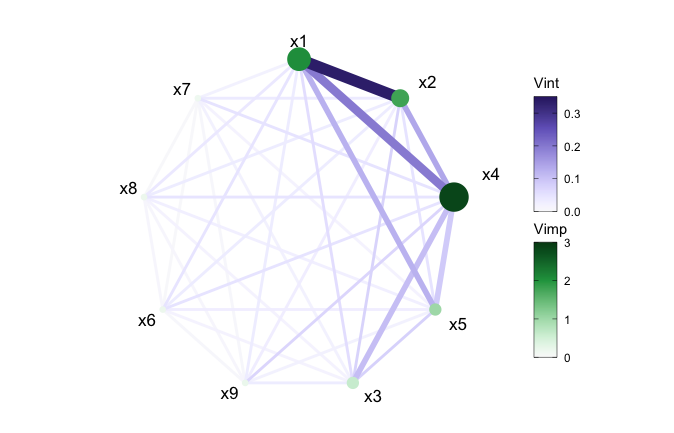

Figure 2: Network plot of a random forest fit displaying 2-way interaction strength and individual variable importance. \(x_1\) and \(x_2\) show a strong interaction with \(x_4\) being the most important for predicting \(y\).

We can also filter out any interactions below a set value using the intThreshold argument. This can be useful when the number of variables included in the model is large or just to highlight the strongest interactions. By default, unconnected nodes are displayed, however, they can be removed by setting the argument removeNode = T.

viviNetwork(mat = viviRf, intThreshold = 0.12, removeNode = FALSE)
viviNetwork(mat = viviRf, intThreshold = 0.12, removeNode = TRUE)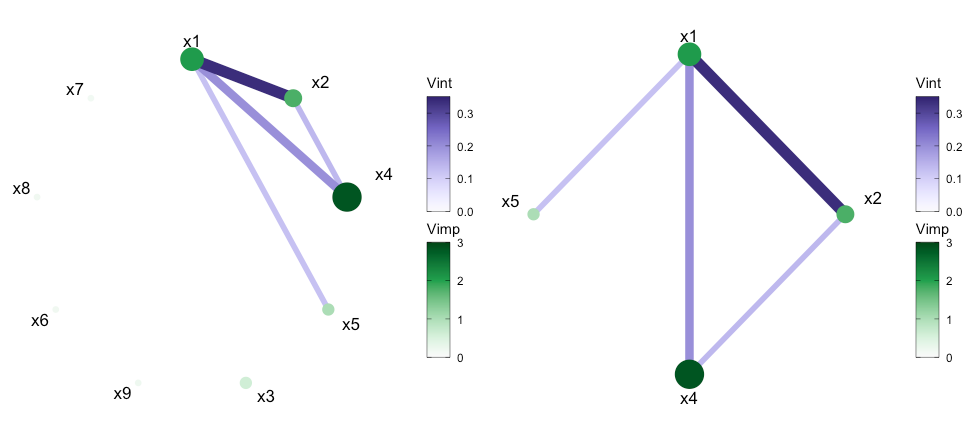

Figure 3: Network plot of a random forest fit displaying 2-way interaction strength and individual variable importance. In (a) a filtered network is shown displaying all interactions above 0.12, with all nodes shown. In (b) the unconnected nodes are removed.

The network plot offers multiple customization possibilities when it comes to displaying the network style plot through use of the layout argument. The default layout is a circle but the argument accepts any igraph layout function or a numeric matrix with two columns, one row per node.

viviNetwork(mat = viviRf, 
            layout = cbind(c(1,1,1,1,2,2,2,2,2), c(1,2,4,5,1,2,3,4,5)))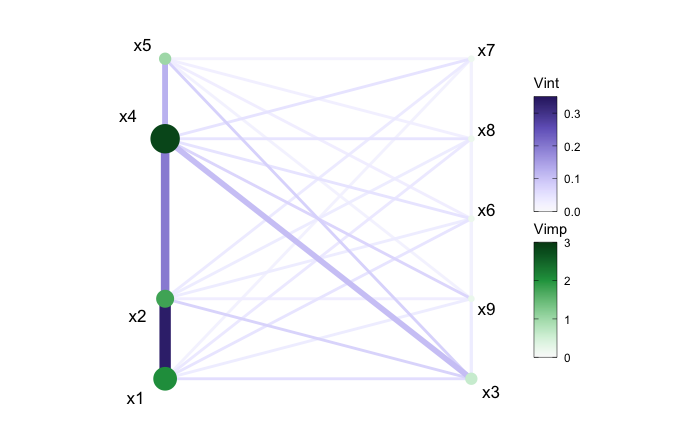

Figure 4: Network plot of a random forest fit using custom layout.

Finally, for the network plot to highlight any relationships in the model fit, we can cluster variables together using the cluster argument. This argument can either accept a vector of cluster memberships for nodes or an igraph package clustering function. In the following example, we manually select variables with VIVI values in the top 20%. This selection allows us to focus only on the variables with the most impact on the response. The variables that remain are \(x1\) to \(x5\). We then perform a hierarchical clustering treating variable interactions as similarities, with the goal of grouping together high-interaction variables. Here we manually select the number of groups we want to show via the cutree function (which cuts clustered data into a desired number of groups). Finally we rearrange the layout using igraph. Here, igraph::layout_as_star places the first variable (deemed most relevant using the VIVI seriation process) at the center, which in Figure 5 emphasizes its key role as the most important predictor which also has the strongest interactions.

set.seed(1701)
# clustered and filtered network for rf
intVals <- viviRf
diag(intVals) <- NA 


# select VIVI values in top 20%
impTresh <- quantile(diag(viviRf),.8)
intThresh <- quantile(intVals,.8,na.rm=TRUE)
sv <- which(diag(viviRf) > impTresh |
              apply(intVals, 1, max, na.rm=TRUE) > intThresh)

h <- hclust(-as.dist(viviRf[sv,sv]), method="single")

viviNetwork(viviRf[sv,sv],
            cluster = cutree(h, k = 3), # specify number of groups
            layout = igraph::layout_as_star)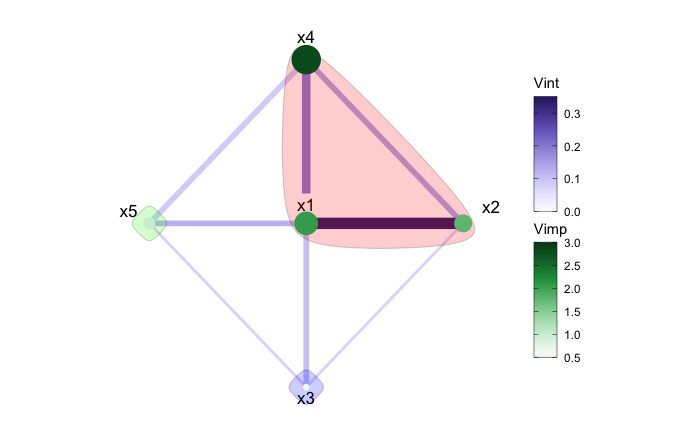

Figure 5: Clustered network plot of a random forest fit.

In Figure 5, after applying a hierarchical clustering, we can see the strongest mutual interactions have been grouped together. Namley; \(x1\), \(x2\), and \(x4\). The remaining variables are individually clustered.

Univariate Partial Dependence Plot

The pdpVars function constructs a grid of univariate PDPs with ICE curves for selected variables. We use ICE curves to assist in the identification of linear or non-linear effects. The fit, data frame used to train the model, and the name of the response variable are required inputs.

In the example below, we select the first five variables from our created vivid matrix to display and set the number of ICE curves to be displayed to be 100, via the nIce argument.

top5 <- colnames(viviRf)[1:5]
pdpVars(data = myData,
        fit = rf,
        response = 'y',
        vars = top5,
        nIce = 100)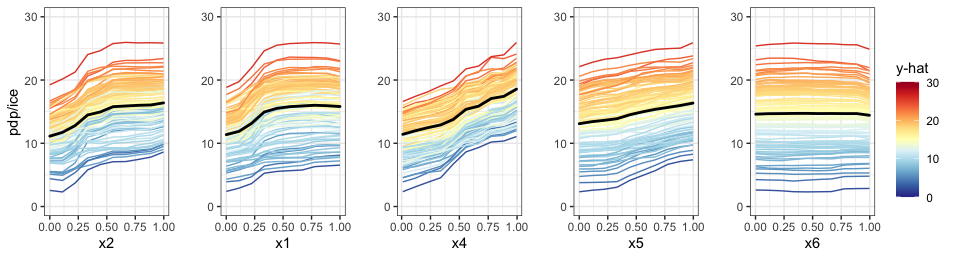

Figure 6: Partial dependence plots (black line) with individual conditional expectation curves (colored lines) of a random forest fit on the Friedman data. The changing partial dependence and ICE curves of \(x1\), \(x2\), and \(x4\) indicate that these variables have some impact on the response.

Generalized partial dependence pairs plot

By employing a matrix layout, the pdpPairs function generates a generalized pairs partial dependence plot (GPDP) that encompasses univariate partial dependence (with ICE curves) on the diagonal, bivariate partial dependence on the upper diagonal, and a scatterplot of raw variable values on the lower diagonal, where all colours are assigned to points and ICE curves by the predicted \(\hat{y}\) value. As with the univariate PDP, the fit, data frame used to train the model, and the name of the response variable are required inputs. For a full description of all the function arguments, see ?vivid::pdpPairs. In the following example, we select the first five variables to display and set the number of shown ICE curves to 100.

set.seed(1701)
pdpPairs(data = myData, 
         fit =  rf, 
         response = "y", 
         nmax = 500, 
         gridSize = 10,         
         vars = c("x1", "x2", "x3", "x4", "x5"),
         nIce = 100)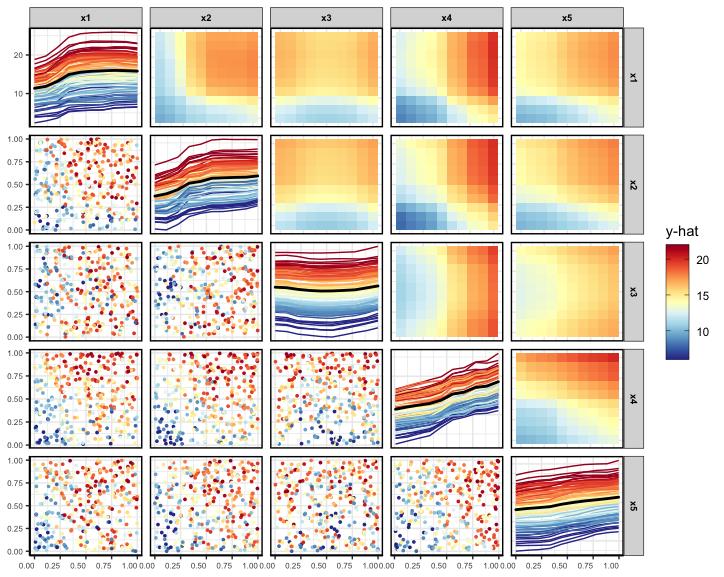

Figure 7: Filtered generalized pairs partial dependence plot for a random forest fit on the Friedman data. From both the univariate and bivariate PDPs, we can see that \(x1\), \(x2\), and \(x4\) have an impact on the response.

Partial dependence ‘Zenplot’

The pdpZen function utilizes a space-saving technique based on graph Eulerians, introduced by Hierholzer and Wiener in 1873[25] to create partial dependence plots. We refer to these plots as zen-partial dependence plots (ZPDP). These plots are based on zigzag expanded navigation plots, also known as zenplots, which are available in the zenplots package[26]. Zenplots were designed to showcase paired graphs of high-dimensional data with a focus on the most significant 2D displays. In our version, we display bivariate PDPs that emphasize variables with the most significant interaction values in a compact zigzag layout. This format is useful when dealing with high-dimensional predictor space.

To begin, we show a ZPDP using all the variables in the model.

set.seed(1701)
pdpZen(data = myData, fit = rf, response = "y", nmax = 500, gridSize = 10)

Figure 8: Zen partial dependence plot for the random forest fit on the Friedman data. Here we display all the variables used in the random forest model.

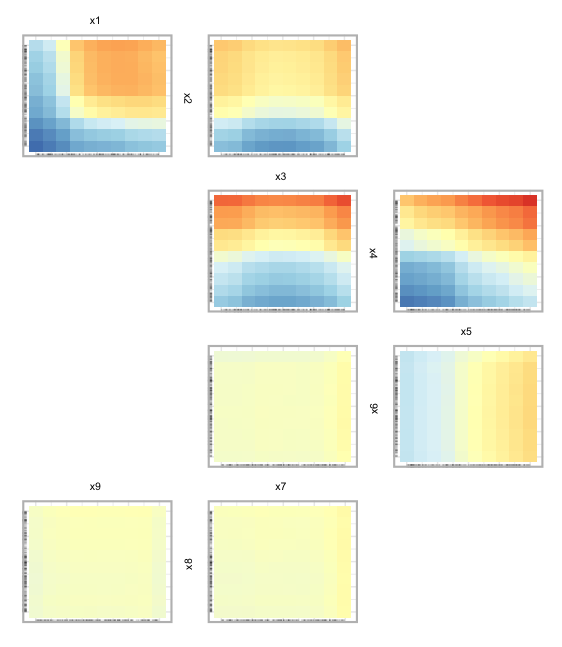
In Fig 8, we can see PDPs laid out in a zigzag structure, with the most influential variable pairs displayed at the top and generally decreasing as we move down. In Figure 9, below, we select a subset of variables to display. In this case we select the first five variables from the data. The argument zpath specifies the variables to be plotted, defaulting to all dataset variables aside from the response.

set.seed(1701)
pdpZen(data = myData, 
       fit = rf, 
       response = "y",
       nmax = 500, 
       gridSize = 10, 
       zpath = c("x1", "x2", "x3", "x4", "x5"))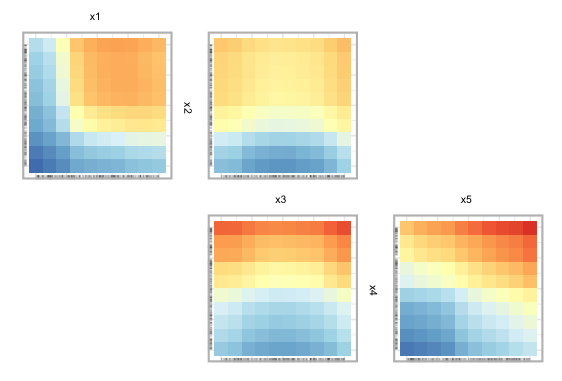

Figure 9: Zen partial dependence plot for the random forest fit on the Friedman data. Here we display only the first five variables.

We can also create a sequence or sequences of variable paths for use in pdpZen. via the zPath function. The zPath function takes four arguments. These are: viv - a matrix of interaction values, cutoff - exclude interaction values below this threshold, method - a string indicating which method to use to create the path, and connect - a logical value indicating if separate Eulerians should be connected.

You can choose between two methods when using the zPath function: "greedy.weighted" and "strictly.weighted". The first method utilizes a greedy Eulerian path algorithm for connected graphs. This method traverses each edge at least once, beginning at the highest-weighted edge, and moving on to the remaining edges while prioritizing the highest-weighted edge. If the graph has an odd number of nodes, some edges may be visited more than once, or additional edges may be visited. The second method, "strictly.weighted" visits edges in strictly decreasing order by weight (in this case, interaction values). If the connect argument is set to TRUE, the sequences generated by the strictly weighted method are combined to create a single path. In the code below, we provide an example of creating zen-paths using the "strictly.weighted" method, from the top 10% of interaction scores in viviRf (i.e., the created vivid matrix.)

# set zpaths with different parameters
intVals <- viviRf
diag(intVals) <- NA
intThresh <- quantile(intVals, .90, na.rm=TRUE)
zpSw <- zPath(viv = viviRf, cutoff = intThresh, connect = FALSE, method = 'strictly.weighted')



set.seed(1701)
pdpZen(data = myData, 
       fit = rf, 
       response = "y",
       nmax = 500, 
       gridSize = 10, 
       zpath = zpSw)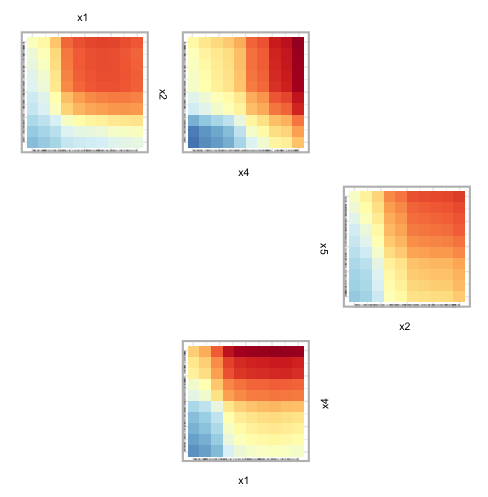

Figure 10: ZPDP for a random forest fit on the Friedman data. The sorting method is defined by the ’strictly.weighted‘ method and is un-connected.

Custom Predict Function

Example using the predict function

We supply an internal custom predict function called CVpredictfun to both importance and interaction calculations. CVpredictfun is a wrapper around CVpredict from the condvis2 package[27]. CVpredict accepts a broad range of fit classes thus streamlining the process of calculating variable importance and interactions. In situations where the fit class is not handled by CVpredict, supplying a custom predict function to the vivi function by way of the predictFun argument allows the agnostic VIVI values to be calculated. For an example of using vivid with many different types of models, see the Section Model Fits In the following, we provide a small example of using such a fit with vivid by using the xgboost package to create a gradient boosting machine (GBM). To begin we build the model.

library("xgboost")
gbst <- xgboost(data = as.matrix(myData[,1:9]),
                label =  as.matrix(myData[,10]),
                nrounds = 100,
                verbose = 0)

We then build the vivid matrix for the GBM fit using a custom predict function, which must be of the form given in the code snippet. Note that the term data must be used in the custom predict function. Do not use the actual name of the data. Additionally, the response variable should be included when generating the predict function for xgboost.

# predict function for GBM
pFun <- function(fit, data, ...) predict(fit, as.matrix(data[,1:9]))

set.seed(1701)
viviGBst <- vivi(fit = gbst,
                 data = myData,
                 response = "y",
                 reorder = FALSE,
                 normalized = FALSE,
                 predictFun = pFun,
                 gridSize = 50,
                 nmax = 500)

From this we can now create our visualisations. For brevity, we only show the heatmap.

viviHeatmap(mat = viviGBst)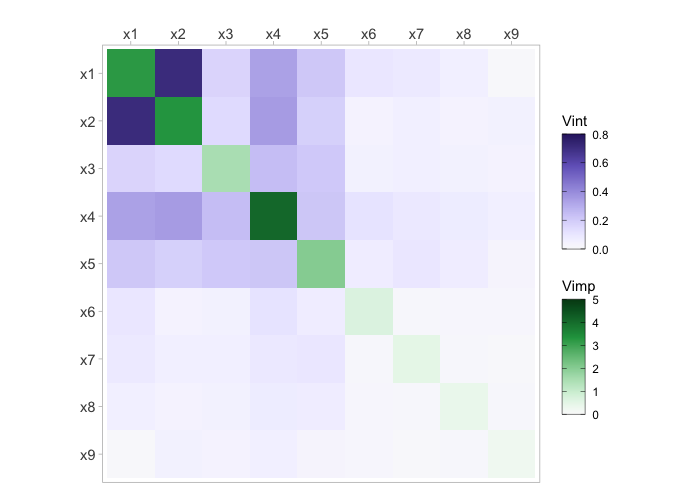

Figure 11: Heatmap for the GBM fit on the Friedman data.

Embedded Vimps

Using embedded importance metrics

In the following we show examples of how to select different (embedded) importance metrics for use with the vivi function. To illustrate the process we use a random forest model fit using the randomForest and ranger packages.

In randomForest

To begin we fit the randomForest model.

set.seed(1701)
rfEmbedded <- randomForest(y ~ ., data = myData, importance = TRUE)

Note that for a randomForest model, if the argument importance = TRUE, then multiple importance metrics are returned. In this case, as we have a regression random forest, the returned importance metrics are the percent increase in mean squared error (%IncMSE) and the increase in node purity (IncNodePurity). In order to choose a specific metric for use with vivid, it is necessary to specify one of the importance metrics returned by the random forest as the argument for the importanceType parameter in the vivi function. In the code below we select the %IncMSE as the importance metric.

viviRfEmbedded <- vivi(fit = rfEmbedded, 
                       data = myData, 
                       response = "y",
                       importanceType = "%IncMSE")

In ranger

For a ranger random forest model, the importance metric must be specified when fitting the model. In the code below, we select the impurity as the importance metric.

library("ranger")
rang <- ranger(y~., data = myData, importance = 'impurity')

Then when calling the vivi function, the importanceType argument is set to the same selected importance metric.

viviRangEmbedded <- vivi(fit = rang, 
                         data = myData, 
                         response = "y",
                         importanceType = "impurity")

Model Fits

Models Used

Additional examples are shown for several different machine learning models (See Articles tab above). These scripts are designed as a quick-stop guide of how to use some of the more popular machine learning R packages with vivid and to familiarize the user with implementing vivid. See individual vignette scripts for specific models. As previously discussed, vivid will work out-of-the-box with several of these R packages, however, with others, a custom predict function will have to be supplied. The packages (and models) shown here are:

• caret - Neural Network
• randomForest - Random Forest
• ranger - Random Forest
• e1071 - Support Vector Machine
• gbm - Gradient Boosted Machine
• mlr3 - k-nearest Neighbours
• xgboost - eXtreme Gradient Boosting
• bartMachine - BART
• keras - Neural Network

Classification

Classification example

In this section, we briefly describe how to apply the above visualisations to a classification example using the iris data set.

To begin we fit a ranger random forest model with “Species” as the response and create the vivi matrix setting the category for classification to be “setosa” using class.

vivi

set.seed(1701)
rfClassif <- ranger(Species~ ., data = iris, probability = T, 
                    importance = "impurity")

set.seed(101)
viviClassif  <- vivi(fit = rfClassif, 
                     data = iris, 
                     response = "Species",
                     gridSize = 10,
                     nmax = 50,
                     reorder = TRUE,
                     class = "setosa")

Heatmap

Next we plot the heatmap and network plot of the iris data.

viviHeatmap(mat = viviClassif)
viviNetwork(mat = viviClassif)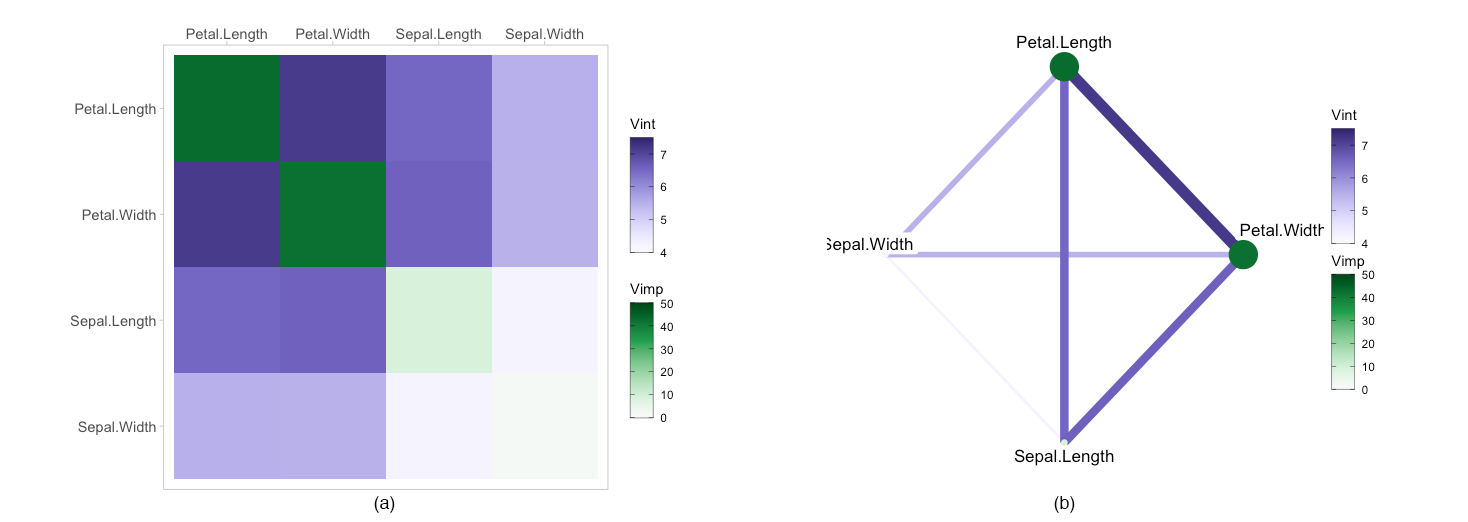

Figure 12: Heatmap in (a) and Network plot in (b) of random forest fit on the iris data

GPDP

As mentioned above, as PDPs are evaluated on a grid and can extrapolate where there is no data. To solve this issue we calculate a convex hull around the data and remove any points that fall outside the convex hull, as shown below.

set.seed(1701)
pdpPairs(data = iris, 
         fit = rfClassif, 
         response = "Species",
         class = "setosa",  
         convexHull = T, 
         gridSize = 10, 
         nmax = 50)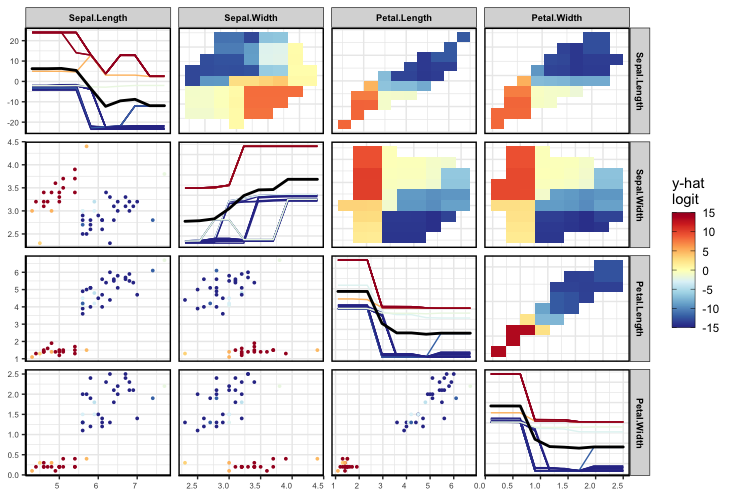 

Figure 12: GPDP of random forest fit on the iris data with extrapolated data removed.

Full Script

This section consolidates the Sections Data and Model, vivi, Visualisations Custom Predict Function, and Embedded Vimps into a single script to facilitate ease of viewing.

# Load libraries
library("vivid") 
library("randomForest")

# Create data based on the Friedman equation
set.seed(101)
genFriedman <- function(noFeatures = 10, noSamples = 100, sigma = 1) {
  
  # Create dataframe with named columns
  df <- setNames(as.data.frame(matrix(runif(noSamples * noFeatures, 0, 1), nrow = noSamples), 
                               stringsAsFactors = FALSE), 
                 paste0("x", 1:noFeatures))
  
  # Equation: y = 10sin(πx1x2) + 20(x3−0.5)^2 + 10x4 + 5x5 + ε
  
  df$y <- 10 * sin(pi * df$x1 * df$x2) + 
    20 * (df$x3 - 0.5)^2 + 
    10 * df$x4 + 
    5 * df$x5 + 
    rnorm(noSamples, sd = sigma) # error
  
  return(df)
}

myData <- genFriedman(noFeatures = 9, noSamples = 350, sigma = 1) 

-------------------------------------------------------------------
  
# Fit random forest using randomForest package
set.seed(1701)
rf <- randomForest(y ~ ., data = myData)

-------------------------------------------------------------------

# Run vivid
set.seed(1701)
viviRf  <- vivi(fit = rf, 
                data = myData, 
                response = "y",
                gridSize = 50,
                importanceType = "agnostic",
                nmax = 500,
                reorder = TRUE,
                predictFun = NULL,
                numPerm = 4,
                showVimpError = FALSE)

-------------------------------------------------------------------

# Visualisations:
  
# 1.0: Heatmap
viviHeatmap(mat = viviRf)

# 1.1: Heatmap with custom colour palettes and a small border around the diagonal importance values
viviHeatmap(mat = viviRf,
            intPal = colorspace::sequential_hcl(palette = "Oslo", n = 100),
            impPal = rev(colorspace::sequential_hcl(palette = "Reds 3", n = 100)),
            border = T)

# 2.0: Network
viviNetwork(mat = viviRf)

# 2.1: Network with interactions below 0.12 are filtered. 
# By default, unconnected nodes are displayed, however, they can be removed by setting `removeNode = T`
viviNetwork(mat = viviRf, intThreshold = 0.12, removeNode = FALSE)
viviNetwork(mat = viviRf, intThreshold = 0.12, removeNode = TRUE)

# 2.3: Network clustered and with interactions thresholded
set.seed(1701)
# clustered and filtered network for rf
intVals <- viviRf
diag(intVals) <- NA 


# select VIVI values in top 20%
impTresh <- quantile(diag(viviRf),.8)
intThresh <- quantile(intVals,.8,na.rm=TRUE)
sv <- which(diag(viviRf) > impTresh |
              apply(intVals, 1, max, na.rm=TRUE) > intThresh)

h <- hclust(-as.dist(viviRf[sv,sv]), method="single")

# plot
viviNetwork(viviRf[sv,sv],
            cluster = cutree(h, k = 3), # specify number of groups
            layout = igraph::layout_as_star)

# 3.0: PDP of the top 5 variables extracted from the vivi matrix and number of ICe curves set to 100
top5 <- colnames(viviRf)[1:5]
pdpVars(data = myData,
        fit = rf,
        response = 'y',
        vars = top5,
        nIce = 100)

# 4.0: GPDP of the variables x1 to x5, with 100 ICE curves shown. 
set.seed(1701)
pdpPairs(data = myData, 
         fit =  rf, 
         response = "y", 
         nmax = 500, 
         gridSize = 10,         
         vars = c("x1", "x2", "x3", "x4", "x5"),
         nIce = 100)

# 5.0: ZPDP of all variables
set.seed(1701)
pdpZen(data = myData, fit = rf, response = "y", nmax = 500, gridSize = 10)

# 5.1: ZPDP where the `zpath` argument specifies the variables to be plotted. In this case, x1 to x5.
set.seed(1701)
pdpZen(data = myData, 
       fit = rf, 
       response = "y",
       nmax = 500, 
       gridSize = 10, 
       zpath = c("x1", "x2", "x3", "x4", "x5"))

# 5.2: ZPDP with the zpaths set with different parameters using the `zPath` function.
intVals <- viviRf
diag(intVals) <- NA
intThresh <- quantile(intVals, .90, na.rm=TRUE)
zpSw <- zPath(viv = viviRf, cutoff = intThresh, connect = FALSE, method = 'strictly.weighted')

set.seed(1701)
pdpZen(data = myData, 
       fit = rf, 
       response = "y",
       nmax = 500, 
       gridSize = 10, 
       zpath = zpSw)

Using a custom predict function

library("vivid")
library("xgboost")
gbst <- xgboost(data = as.matrix(myData[,1:9]),
                label =  as.matrix(myData[,10]),
                nrounds = 100,
                verbose = 0)

# predict function for GBM
pFun <- function(fit, data, ...) predict(fit, as.matrix(data[,1:9]))

# run vivid
set.seed(1701)
viviGBst <- vivi(fit = gbst,
                 data = myData,
                 response = "y",
                 reorder = FALSE,
                 normalized = FALSE,
                 predictFun = pFun,
                 gridSize = 50,
                 nmax = 500)

# plot heatmap
viviHeatmap(mat = viviGBst)

Using embedded variable importance

library("vivid")
library("randomForest")
library("ranger")

# randomForest
# Note importance must be set to TRUE to use embedded importance scores. 
set.seed(1701)
rfEmbedded <- randomForest(y ~ ., data = myData, importance = TRUE)

# Using % increase in MSE as the importance metric in vivid
viviRfEmbedded <- vivi(fit = rfEmbedded, 
                       data = myData, 
                       response = "y",
                       importanceType = "%IncMSE")

# Plot Heatmap
viviHeatmap(mat = viviRfEmbedded)

# ranger
# Note the importance metric is selected directly in ranger
rang <- ranger(y~., data = myData, importance = 'impurity')

# Run vivid
viviRangEmbedded <- vivi(fit = rang, 
                         data = myData, 
                         response = "y",
                         importanceType = "impurity")

# Plot Heatmap
viviHeatmap(mat = viviRangEmbedded)

Classification

library("vivid")
library("randomForest")

set.seed(1701)
rfClassif <- ranger(Species~ ., data = iris, probability = T, 
                    importance = "impurity")

set.seed(101)
viviClassif  <- vivi(fit = rfClassif, 
                     data = iris, 
                     response = "Species",
                     gridSize = 10,
                     nmax = 50,
                     reorder = TRUE,
                     class = "setosa")

viviHeatmap(mat = viviClassif)

set.seed(1701)
pdpPairs(data = iris, 
         fit = rfClassif, 
         response = "Species",
         class = "setosa",  
         convexHull = T, 
         gridSize = 10, 
         nmax = 50) 

References

1. Alan Inglis and Andrew Parnell and Catherine B. Hurley (2022) Visualizing Variable Importance and Variable Interaction Effects in Machine Learning Models. Journal of Computational and Graphical Statistics (3), pages 1-13

2. Breiman, Leo. 2001. “Random Forests.” Machine Learning 45 (1): 5–32. https://doi.org/10.1023/A: 1010933404324.

3. Friedman, J. H. 2000. “Greedy Function Approximation: A Gradient Boosting Machine.” The Annals of Statistics 29 (November). https://doi.org/10.1214/aos/1013203451.

4. Chipman, Hugh A, Edward I George, and Robert E McCulloch. 2010. “BART: Bayesian Additive Regression Trees.” The Annals of Applied Statistics 4 (1): 266–98.

5. Paluszynska, Aleksandra, Przemyslaw Biecek, and Yue Jiang. 2020. randomForestExplainer: Explaining and Visualizing Random Forests in Terms of Variable Importance. https://CRAN.R-project.org/ package=randomForestExplainer.

6. Ishwaran, Hemant, Udaya B Kogalur, Eiran Z Gorodeski, Andy J Minn, and Michael S Lauer. 2010. “High-Dimensional Variable Selection for Survival Data.” Journal of the American Statistical Associa- tion 105 (489): 205–17.

7. Probst, Philipp. 2020. varImp: RF Variable Importance for Arbitrary Measures. https://CRAN.R-project. org/package=varImp.

8. Strobl, Carolin, Anne-Laure Boulesteix, Thomas Kneib, Thomas Augustin, and Achim Zeileis. 2008. “Conditional Variable Importance for Random Forests.” BMC Bioinformatics 9 (307). https://doi. org/10.1186/1471-2105-9-307

9. Maksymiuk, Szymon, Ewelina Karbowiak, and Przemyslaw Biecek. 2021. EIX: Explain Interactions in ’XGBoost’. https://CRAN.R-project.org/package=EIX.

10. Molnar, Christoph, Bernd Bischl, and Giuseppe Casalicchio. 2018. “Iml: An r Package for Interpretable Machine Learning.” JOSS 3 (26): 786. https://doi.org/10.21105/joss.00786.

11. Mayer M (2023). flashlight: Shed Light on Black Box Machine Learning Models. R package version 0.9.0, https://CRAN.R-project.org/package=flashlight.

12. Biecek, Przemyslaw. 2018. “DALEX: Explainers for Complex Predictive Models in R.” Journal of Machine Learning Research 19 (84): 1–5. https://jmlr.org/papers/v19/18-416.html.

13. Greenwell, Brandon M., and Bradley C. Boehmke. 2020. “Variable Importance Plots—an Introduction to the vip Package.” The R Journal 12 (1): 343–66. https://doi.org/10.32614/RJ-2020-013.

14. Fisher A., Rudin C., Dominici F. (2018). All Models are Wrong but many are Useful: Variable Importance for Black-Box, Proprietary, or Misspecified Prediction Models, using Model Class Reliance. Arxiv.

15. Marvin N. Wright, Andreas Ziegler (2017). ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. Journal of Statistical Software, 77(1), 1-17. doi:10.18637/jss.v077.i01], randomForest^[A. Liaw and M. Wiener (2002). Classification and Regression by randomForest. R News 2(3), 18–22.

16. Bischl B, Lang M, Kotthoff L, Schiffner J, Richter J, Studerus E, Casalicchio G, Jones Z (2016). “mlr: Machine Learning in R.” Journal of Machine Learning Research, 17(170), 1-5. https://jmlr.org/papers/v17/15-066.html.

17. Lang M, Binder M, Richter J, Schratz P, Pfisterer F, Coors S, Au Q, Casalicchio G, Kotthoff L, Bischl B (2019). “mlr3: A modern object-oriented machine learning framework in R.” Journal of Open Source Software. doi:10.21105/joss.01903

18. Kuhn M, Vaughan D (2023). parsnip: A Common API to Modeling and Analysis Functions. R package version 1.1.1, https://CRAN.R-project.org/package=parsnip.

19. Friedman, J. H. 2000. “Greedy Function Approximation: A Gradient Boosting Machine.” The Annals of Statistics 29 (November). https://doi.org/10.1214/aos/1013203451.

20. Goldstein, Alex, Adam Kapelner, Justin Bleich, and Emil Pitkin. 2015. “Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation.” Journal of Computational and Graphical Statistics 24 (1): 44–65. https://doi.org/10.1080/10618600.2014. 907095.

21. Greenwell, Brandon M. 2017. “pdp: An r Package for Constructing Partial Dependence Plots.” The R Journal 9 (1): 421–36. https://journal.r-project.org/archive/2017/RJ-2017-016/index.html.

22. Friedman, J. H. and Popescu, B. E. (2008). “Predictive learning via rule ensembles.” The Annals of Applied Statistics. JSTOR, 916–54.

23. Friedman, Jerome H. (1991) Multivariate adaptive regression splines. The Annals of Statistics 19 (1), pages 1-67.

24. Zeileis, Achim, Jason C. Fisher, Kurt Hornik, Ross Ihaka, Claire D. McWhite, Paul Murrell, Reto Stauffer, and Claus O. Wilke. 2020. “Colorspace: A Toolbox for Manipulating and Assessing Colors and Palettes.” Journal of Statistical Software, Articles 96 (1): 1–49

25. Hierholzer, Carl, and Chr Wiener. 1873. “Über Die möglichkeit, Einen Linienzug Ohne Wiederholung Und Ohne Unterbrechung Zu Umfahren.” Mathematische Annalen 6 (1): 30–32.

26. Hofert, Marius, and Wayne Oldford. 2020. “Zigzag Expanded Navigation Plots in R: The R Package zenplots.” Journal of Statistical Software 95 (4): 1–44.

27. Hurley, Catherine, Mark OConnell, and Katarina Domijan. 2022. Condvis2: Interactive Conditional Visualization for Supervised and Unsupervised Models in Shiny.